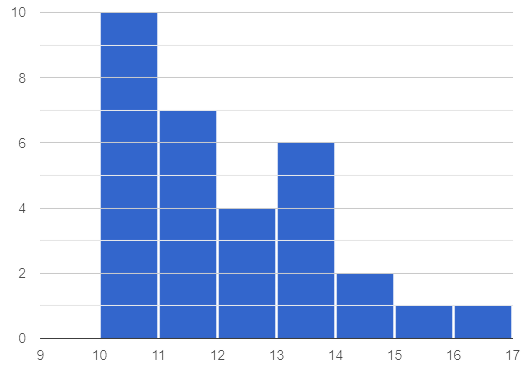
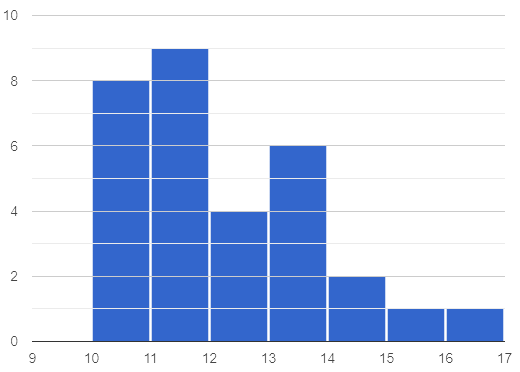
1 The two histograms below show the number of minutes students spent traveling to school: one represents a sample of sixth grade students and the other represents a sample of eighth grade students. All travel times in the dataset are whole numbers.
Distribution of Travel Times (Sixth Grade)
|
Distribution of Travel Times (Eighth Grade)
|
2 Which group has the larger mode(s). sixth graders eighth graders the modes are roughly the same
Students might choose 6th graders because the tallest bin has 10, whereas the tallest 8th grade bin has 9… but we’re looking for which value the tallest bin lands on, which is between 10 and 15 for 8th graders and between 5 and 10 for sixth graders.
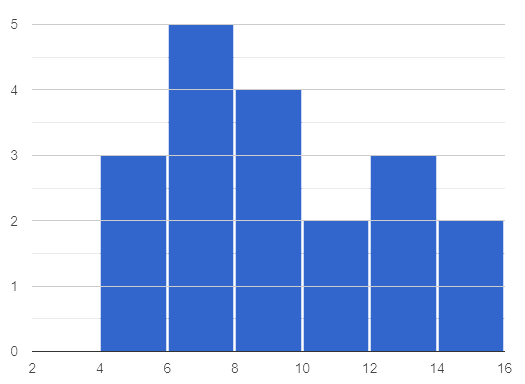
3 The histogram below shows the ages of the 19 children who signed up for rock climbing camp.
Distribution of Rock Climbers' Ages
|
The median age for these 19 climbers is:
☐ about 6 or 7
☐ about 8 or 9
☐ about 10 or 11
☐ about 12 or 13 |
Explain how you determined the median value:
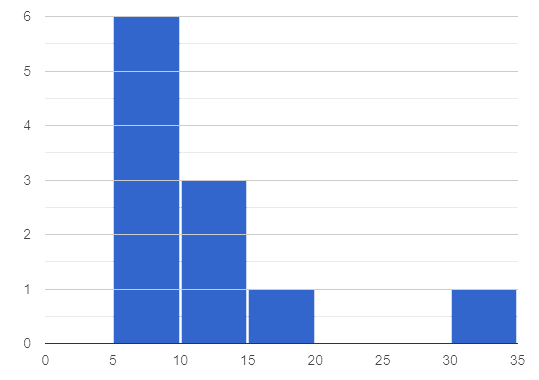
4 Eleven students were asked to solve a logic puzzle. The minimum time was 5 minutes, and the maximum time was 35 minutes. The distribution of their times is shown on the histogram below.
Distribution of Time Spent Solving a Logic Puzzle
|
Which of the following statements is likely a correct comparison of the mean and median number of minutes spent working?
☐ The mean time is less than the median time.
☐ The mean time is equal to the median time.
☐ The mean time is greater than the median time.
☐ There isn’t enough information provided to determine which is greater. |
Explain how you arrived at your choice:
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). 
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.