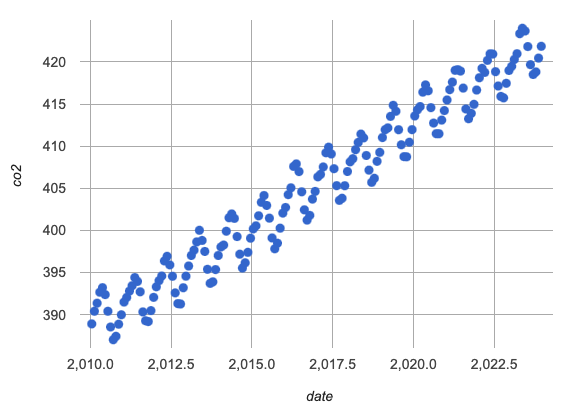
This page focuses on the modern-table of the Hybrid CO2 Models Starter File, which tracks atmospheric CO2 (parts per million) from 2010-2023.
Decomposing Your Periodic Model
Towards the bottom of the Definitions Area, find the section of the starter file where you’re asked to "Define your periodic-sin functions…"
1 Define periodic-sin to be the periodic model you found earlier, for CO2 levels from 2022-2023.
-
You should already have defined it in Carbon Dioxide Starter File.
-
You can also look at Modeling Recent Carbon Dioxide Levels (continued), the workbook page from the previous lesson.
2 Using the deconstruction of periodic-cos as your model, change the other three functions in this section to show how to separate the wave and midline of your periodic-sin model and define periodic-sin2 using function composition.
Fitting the Optimal Linear Model
3 Use fun linear-modern(x): ( * x) + end
4 Change the The S-value is:
5 Sketch the model on the graph to the right. |
|
Fitting your Periodic Model
6 Use The S-value is:
7 Sketch the model on the graph to the right. What would need to change about your model, to fit this data?
|
|
Imagining the Best Possible Model
8 Sketch the best possible model you can imagine for this data on the graph to the right, and describe it. Do parts of it look linear? Quadratic? Exponential? Logarithmic? Periodic? |
|
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). 
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.