instagram

Students discover functions as an abstraction over a programming pattern, and are introduced to a structured approach to building them called the Design Recipe.

Prerequisites

Defining Values

Lesson Goals

Students will be able to:

  • Describe the usefulness of functions.

  • Create their own functions and examples given the constraints of a problem.

Student-Facing Lesson Goals

  • I can explain why a function is useful.

  • I can plan and create my own function with examples.

Materials

Preparation

  • Make sure all materials have been gathered

  • Decide how students will be grouped in pairs

Key Points for the Facilitator

  • This lesson represents a big shift in thinking. After some practice, students will not be limited to pre-existing functions!

  • Take plenty of time for the Design Recipe as students will return to it frequently in future lessons.

Click here to see the prior unit-based version

Glossary
contract

a statement of the name, domain, and range of a function

definitions area

the left-most text box in the Editor where definitions for values and functions are written

design recipe

a sequence of steps that helps people document, test, and write functions

example

shows the use of a function on specific inputs and the computation the function should perform on those inputs

function

a mathematical object that consumes inputs and produces an output

Number

a data type representing a real number

syntax

the set of rules that defines a language, whether it be spoken, written, or programmed.

🔗Identifying Repeated Patterns 30 minutes

Overview

As with the Defining Values lesson, students search for structure in a list of expressions. But this time, the structures are dynamic, meaning they change in a predictable way. This is the foundation for defining functions.

Launch

Students should have their workbook, pencil, and be logged into code.pyret.org on their computer.

I Love Green Triangles I Love Green Triangles🖼Show image

I Love Green Triangles I Love Green Triangles🖼Show image

Confess to your students, "I LOVE green triangles." Challenge them to use the Definitions area to make as many DIFFERENT solid green triangles as they can in 2 minutes.

Walk around the room and give positive feedback on the green triangles. After the 2 minutes, ask for some examples of green triangles that they wrote and copy them to the board. Be specific and attend to precision with the syntax such that students can visually spot the pattern between the different lines of code.

For example:

triangle(30,  "solid", "green")
triangle(12,  "solid", "green")
triangle(500, "solid", "green")

Notice and Wonder

Direct students to the various lines of code they came up with. What do you notice? What do you wonder?

  • Is there a pattern? Yes, the code mostly stayed the same with one change each time.

  • What stayed the same? The function name triangle, "solid", "green".

  • What changed? The number being given to triangle, or the Number input.

  • What strategy did you use to create many different triangles? Answers vary: Pattern matching, copy and paste

  • What shortcut did we use before when we wanted to use the same code over and over?
    We defined values in the Definitions area.

We’ve learned how to define values when we want to create a shortcut to reuse the same code over and over.

For example:

myStar = star(50, "solid", "gold")

But to make a shortcut that changes such as creating solid, green triangles of a changing size, we need to define a function.

Suppose we want to define a shortcut called gt. When we give it a number, it makes a solid green triangle of whatever size we gave it.

Select a student to act out gt. Make it clear to the class that their Name is "gt", they expect a Number, and they will produce an Image. Run through some sample examples before having the class add their own:

  • You say: gt 20! The student responds: triangle(20, "solid", "green")!

  • You say: gt 200! The student responds: triangle(200, "solid", "green")!

  • You say: gt 99! The student responds: triangle(99, "solid", "green")!

We need to program the computer to be as smart as our volunteer. But how do we do that?

Investigate

Let’s walk through an example of defining gt. Turn to Fast Functions (Page 21).

Word Problem: Write a function called gt that takes in a Number and produces a solid, green triangle of that given size.

Have students follow along on the Fast Functions (Page 21) workbook page.

1. Write the contract for this new function by looking at the word problem.
- What does gt take in?
- A Number

  • What does gt give back?

  • An Image. Students may say "a triangle", follow up by asking what data type that triangle will be (Number, String, or Image)

2. Write some examples of how this function should work. - If I typed gt(40) , what would I want the program to do?
- I’d want the computer the execute the code triangle(40, "solid", "green"). (This is a tough question at first. If students are unsure, remind them that we’re just writing a shortcut for making green triangles so we don’t have to type triangle, "solid", and "green" every time!)

  • OPTIONAL: Have students turn back to Page 20 worksheet, showing how their function examples are working.

3. Circle and Label what is "change-able" - or variable between the examples. Circle and label it with a name that describes it.
The number is changing in each example. We could name it "x", but "size" is a more accurate name.

Circle and label what is changing Circle and label what is changing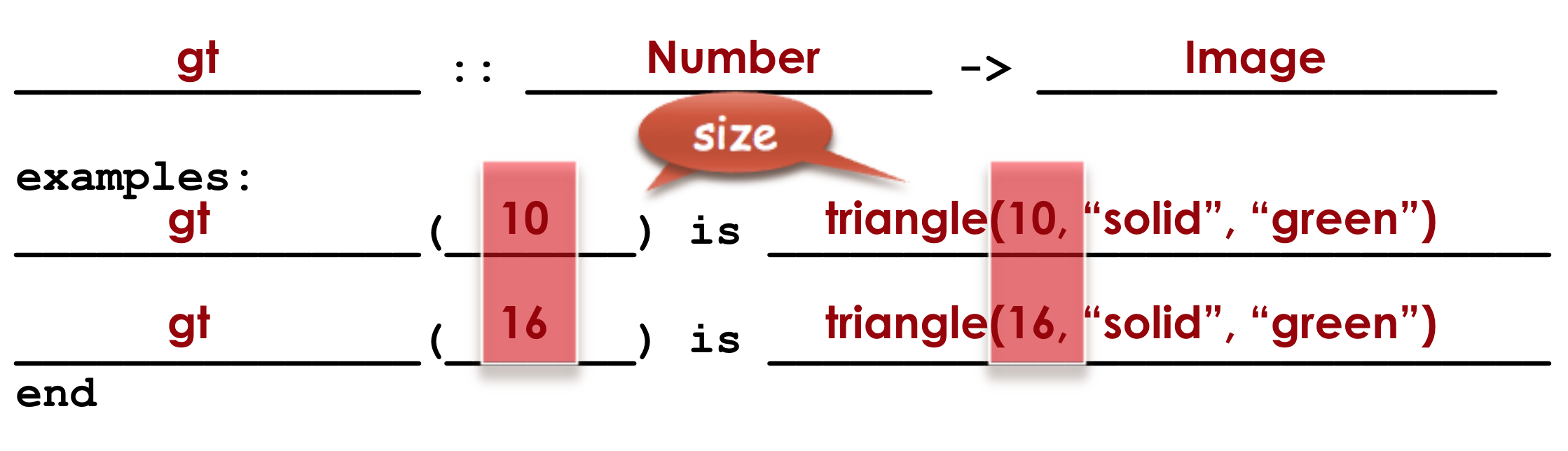🖼Show image

4. Write the function definition.

Look at the two examples. The function definition will follow the same pattern, but it will use the variable name size in place of the variable part we circled. We also use the keyword fun, replace the colon (is) with a colon (:), and finish it off with an end.

fun gt(size): triangle(size, "solid", "green") end

Connecting to Best Practices

- Writing the examples is like "showing your work" in math class.

- Have students circle what is changing and label it with a proper variable name. The name of the variable should reflect what it represents, such as size.

- Writing examples and identifying the variables lays the groundwork for writing the function, which is especially important as the functions get more complex. Don’t skip this step!

Have students type the Contract, Examples, and Definition of gt into a new WeScheme program (in the Definitions Area!), save their program as 'Defining Functions' and test out gt in the Interactions window.

Fast Functions (Page 21) includes another sample problem at the top. Can students fill out the page to define bc?

Synthesize

  • What is the domain for gt? Number

  • Why might someone think the domain for gt contains a Number and two Strings, because that’s the Domain of triangle? The function gt uses triangle, but only needs one Number input because that’s the only part that’s changing.

  • Why is defining functions useful to us as programmers?

🔗Practicing the Design Recipe flexible

Overview

This is a chance for students to independently review the steps learned in the prior activity, with the teacher in a supporting role asking guiding questions and giving support when needed.

Launch

Word Problem: Write a function called gold-star that takes in number and produces a solid, gold star of that given size.

  • Write 2 examples and the definition of gold-star on the 'Fast Functions' handout.

  • Complete the gold-star example on the Fast Functions (Page 21) worksheet.

Investigate

  • Design a problem for a function that takes in one input and returns a shape that uses that input. Your function’s input could be a Number, as in the two examples, or a String.

  • Write two examples and a definition for your function

  • Complete the Mapping Examples with Circles of Evaluation (Page 20) for the examples of your function.

Synthesize

The Design Recipe is a powerful tool for solving word problems. In this lesson, students practiced using it on simple programming problems, but soon they’ll be applying it to traditional math problems. Encourage them to make this connection on their own: can they think of a math problem in which this would be useful?

🔗Additional Exercises:

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, and 1738598). CCbadge Bootstrap:Integrated Oklahoma by Jen Poole is licensed under a Creative Commons 4.0 Unported License. Based on a work at www.BootstrapWorld.org. Permissions beyond the scope of this license may be available by contacting schanzer@BootstrapWorld.org.