Order of Operations

Students experiment with the Editor, exploring the different kinds of numbers and how they behave in this programming language.

Students should open code.pyret.org (CPO) in their browser, and click "Sign In". This will ask them to log in with a valid Google account (Gmail, Google Classroom, YouTube, etc.), and then show them the "Programs" page. This page is empty - they don’t have any programs yet! Have them click "Open Editor".

Our Editing Environment 🖼Show image This screen is called the Editor, and it looks something like the diagram you see here. There are a few buttons at the top, but most of the screen is taken up by two large boxes: the Definitions Area on the left and the Interactions Area on the right.

The Definitions Area is where programmers define values and functions that they want to keep, while the Interactions Area allows them to experiment with those values and functions. This is like writing function definitions on a blackboard, and having students use those functions to compute answers on scrap paper.

Math is a language, just like English, Spanish, or any other language. We use nouns, like "bread", "tomato", "mustard" and "cheese" to describe physical objects. Math has values, like the numbers 1, 2 or 3, to describe quantities.

Our programming language knows about many types of numbers, and they behave pretty much the way they do in math. Our Editor is also pretty smart, and can automatically switch between showing a rational number as a fraction or a decimal, just by clicking on it!

Students are given a challenging expression that exposes common misconceptions about order of operations. The goal is to demonstrate that a brittle, fixed notion of order of operations is not good enough, and lead students to a deeper understanding of Order of Operations as a grammatical device. The Circles of Evaluation are introduced as "sentence diagramming for arithmetic".

Humans also use verbs like "throw", "run", "build" and "jump" to describe operations on these nouns. Mathematics has functions - or "operations" - like addition and subtraction, which are operations performed on values. Just as you can "spread mustard on bread", a person can also "add four and five".

A mathematical expression is like a sentence: it’s an instruction for doing something. The expression 4+5 tells us to add 4 and 5. To evaluate an expression, we follow the instructions in the expression. The expression 4 + 5$\displaystyle 4 + 5$ evaluates to 9.

🖼Show image Sometimes, we need multiple expressions to accomplish a task, and it will matter in which order they come. For exmple, if you were to write instructions for making a sandwich, it would matter very much which instruction came first: melting the cheese, slicing the bread, spreading the mustard, etc. The order of functions matters in mathematics, too.

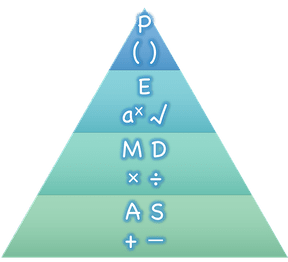
Mathematicians didn’t always agree on the order of operations, but now we have a common set of rules for how to evaluate expressions. The pyramid on the right summarizes the order. When evaluating an expression, we begin by applying the operations written at the top of the pyramid (multiplication and division). Only after we have completed all of those operations can we move down to the lower level. If both operations are present (as in 4 + 2 − 1$\displaystyle 4 + 2 − 1$), we read the expression from left to right, applying the operations in the order in which they appear.

Order of Operations mneumonic devices like PEMDAS, GEMDAS, etc focus on how to get the answer. What we need is a better way to read math.

Instead of a rule for computing answers, let’s start by diagramming the math itself! We can draw the structure of this grammer in mathematics using something called the Circles of Evaluation. The rules are simple:

That means that Numbers (e.g. - 3, -29, 77.01…​) are still written by themselves. It’s only when we want to do something like add, subtract, etc. that we need to draw a Circle.

If we want to draw the Circle of Evaluation for 6 ÷ 3$\displaystyle 6 \div 3$, the division function (/) is written at the top, with the 6 on the left and the 3 on the right.

What if we want to use multiple functions? How would we draw the Circle of Evaluation for 6 ÷ (1 + 2)$\displaystyle 6 \div (1 + 2)$? Drawing the Circle of Evaluation for the 1 + 2$\displaystyle 1 + 2$ is easy. But how do divide 6 by that circle?

Circles can contain other Circles

We basically replace the 3 from our earlier Circle of Evaluation with another Circle, which adds 1 and 2!

Circles of Evaluation help us write code

When converting a Circle of Evaluation to code, it’s useful to imagine a spider crawling through the circle from the left and exiting on the right. The first thing the spider does is cross over a curved line (an open parenthesis!), then visit the operation - also called the function - at the top. After that, she crawls from left to right, visiting each of the inputs to the function. Finally, she has to leave the circle by crossing another curved line (a close parenthesis).

Practice creating Circles of Evaluation using the common operators (+, -, *, /).

Circles of Evaluation help us get the correct answer

Aside from helping us catch mistakes before they happen, Circles of Evaluation are also a useful way to think about transformation in mathematics. For example, you may have heard that "any subtraction can be transformed to a negative addition." For example, 1 - 2$\displaystyle 1 - 2$ can be transformed to 1 + -2$\displaystyle 1 + (-2)$.

Suppose someone tells you that 1 - 2 * 3 + 4$\displaystyle 1 - 2 * 3 + 4$ can be rewritten as 1 + -2 * 3 + 4$\displaystyle 1 + (-2) * 3 + 4$. These two expressions will definitely give us the same answer, but this transformation is actually incorrect! It doesn’t use the negative addition rule at all! Take a moment to think: what’s the problem?

We can use the Circles of Evaluation to figure it out!

The first Circle is just the original expression. The multiplication happens first, so let’s see how multiplication changes this circle:

As you can see, replacing the subtraction with a negative addition happens to the result of the multiplication. We can’t actually change the 2 into a -2, because it isn’t actually being subtracted from 1!

Sure, we got the same answer - but that doesn’t mean the way we got it was correct. If all that mattered was getting the right answer, we could just as easily have replaced the whole expression with 5 - 6$\displaystyle 5 - 6$. And that is definitely not a correct transformation!

Any time you make a transformation in math (replacing 10 - 2$\displaystyle 10 - 2$ with 8$\displaystyle 8$ because of subtraction, or replacing 2 + 6$\displaystyle 2 + 6$ with 6 + 2$\displaystyle 6 + 2$ because of commutativity), you need to make sure the transformation is correct. The Circles of Evaluation help us see these transformation visually, rather than forcing us to keep them in our heads.

The Circles of Evaluation are a great way to visualize other functions you already know, such as square and square root!

Note: In Pyret, we treat operators like +, -, *, and / differently - they are written in between their inputs, just like in math. We also use letters instead of symbols for function names, so taking the square root is written as num-sqrt and squaring is written as num-sqr.