instagram

Students learn to gauge model "fitness" using S value (Standard Deviation of Residuals), building and fitting a variety of linear models to a dataset, first by trial-and-error and then using linear regression.

Lesson Goals

Students will be able to…​

  • Informally assess the fit of a function by plotting and analyzing residuals.

  • Make predictions based upon the equation of the model.

  • Recognize when different kinds of models best describe a situation or data, and use those functions to solve problems and make predictions.

  • Determine line-of-best-fit using linear regression, use regression lines to make predictions, and use model-fit statistics to assess the reliability of those predictions.

Student-facing Lesson Goals

  • Let’s use Pyret to fit linear models to our dataset.

Materials

Supplemental Materials

Preparation

🔗Fitting and Comparing Linear Models

Overview

Students compare the fits of the Alabama-Alaska model and the Michigan-California model. They also have the option of building a Massachusetts-Nevada model and trying to make some better models of their own through trial and error.

Launch

Review: What can we learn from Residuals and S-values? circles back to what students learned in Fitting Models so their understanding of S-values and residuals is fresh.

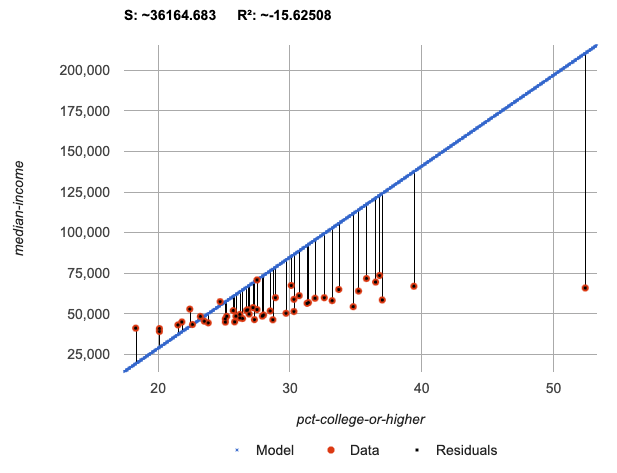a scatter plot displaying percent-college-or-higher (between 17 and 55) on the x-axis and median-income (between 30000 and 75000) on the y-axis. Overlayed on the scatterplot is a blue linear model, sloping upward from 20000 to 215000. There are vertical black lines connecting each data point to the model representing the residuals. We also see S:~36164.683 and R²:~15.62508The al-ak model

  • What does it mean that the S-value for our al-ak model is 36165?

  • We know that there’s enough error in the model to predict median incomes that are off by $36,165!

  • We have to look at the range of the dataset to really know what the S-value means!

  • Considering the range of the data, the error in the model is enough to double the median income of a state or cut it in half!

    • The lowest median incomes are found in Mississippi ($39.031), Arkansas ($40,768), and West Virginia ($41,043).

    • The highest median income is found in Maryland ($73,538).

Compared to the size of the incomes in this dataset, an S value of $36,165 is pretty terrible. This model should not be trusted!

Give students a chance to adjust their al-ak model by trial and error and practice defining a second model using Massachusetts and Nevada by having them complete More Models: College Degrees v. Income.

  • We made a model using Alabama and Alaska. The S-value for this al-ak model is ~36164.683.

  • The ma-nv model was made using Massachusetts and New Nevada. The S-value for the ma-nv model is ~7504.54.

  • What comparisons can we make between these two models?

  • We expect significantly less error in predictions made from the ma-nv model.

  • The S-value of the ma-nv is 28660 dollars less!

  • We expect predictions made with the ma-nv model to 79% less error than predictions made with the al-ak model.

Investigate

Can we do better?

  • The S-value for the al-ak model (made using data points for Alabama and Alaska) is ~36164.683.

  • The S-value for the mi-ca model (made using data points for Michigan and California) is ~10779.923.

  • What comparisons can we make between these two models?

  • We expect significantly less error in predictions made from the mi-ca model.

  • Based on the S-values, we expect prediction made with mi-ca to have about 25385 dollars less error than those made with the al-ak model!

  • We expect predictions made with the mi-ca model to have about 70% less error than predictions made with the al-ak model.

Make sure your students know to how to calculate what percent less error we expect in predictions from the mi-ca model than the al-ak model. Students are about to calculate what percent more or less error we expect from predictions made with their models, which will all have different S-values. Right now everyone is looking at the same S-values so supporting them will be much less work!

Percent Change   =   $$\displaystyle \frac{  \text{Difference}   \text{between}   \text{the}   \text{S-values} } {\text{S-value}   \text{for}   \text{al-ak}   \text{model}} \times 100   =   \frac{25384.76}{36164.683} = .70   →   70 \%$$

For a side by side visual comparison of their models have students complete Graphing Linear Models. Students who did not complete More Models: College Degrees v. Income should just sketch the two models they made.

  • What was the best model (lowest S!) you could come up with?

  • How did your model compare to the al-ak model?

  • When we compared the S-values of the models, why did we divide by the S-value from the al-ak model?

  • Because we were asking how much more or less error we expected in predictions made with our model than with the al-ak model - we were comparing to the al-ak model.

  • If we had divide the change in S by the S-value of our model it would have answered a different question: "How much more or less error do we expect in predictions made with the al-ak model than with our model?"

Going Deeper

For a discussion of why the standard error of the regression S may provide more useful information than R2 , we recommend visiting this link. Further discussion of S and Residuals may be appropriate for older students, or in an AP Statistics class. We also have an entire Bootstrap:Data Science lesson on Standard Deviation.

Synthesize

  • What does it mean if S is zero?

  • The model fits the data perfectly.

  • Is an S-value of 1000 bad?

  • Without more context, we have no way of knowing! S-values only make sense when considered in the alongside the range of the dataset. In our income dataset, 1000 is a pretty good S, because $1000 isn’t a big margin of error. But in a dataset showing the number of students in a school, 1000 would be a very significant error!

🔗Finding the Best Linear Model

Overview

Students are introduced to the lr-plot function in Pyret, which uses linear regression to fit the best possible linear model to the data.

If you want to spend more time with students interpreting regression results, writing about findings, or digging into R2  (a different measure of model fitness), we have an entire Bootstrap: Data Science lesson on Linear Regression.

Launch

We’ve learned how to measure how well linear models fit the data and to decide which linear model does a better job of predicting values. We could keep guessing and picking two points over and over, and our models would likely improve, but we’d never know whether we had found the best possible linear model.

Luckily statisticians have developed an algorithm called linear regression, which, given any dataset, considers every point and produces the best possible linear model, known as the line of best fit.

Pyret’s lr-plot function uses linear regression to graph the best possible linear model on top of a scatter plot of the dataset, and tell us the slope, y-intercept and S-value of the model.

Investigate

Let’s use Pyret to find the best possible linear model for predicting median income of a state from the percent of the population that has attended college.

a scatter plot displaying percent-college-or-higher (between 17 and 55) on the x-axis and median-income (between 30000 and 75000) on the y-axis. Overlayed on the scatterplot is a blue linear model defined as y = 1142.03x + ~20868.1. We also see r:~0.765 R²:~0.585 and S:~5716.667

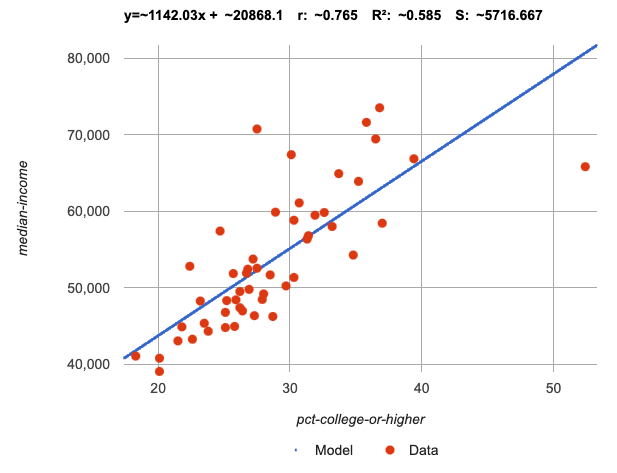
  • How close did your models come to the optimal model?

  • Did anything about the optimal model surprise you?

Synthesize

  • Why is it advantageous to use linear regression to find a model?

  • Instead of focusing on two points, linear regression considers all of the points!

  • We know that we are working with the best possible linear model.

🔗Using and Interpreting our Models

Overview

Students interpret their models, practice using them to make predictions, and consider what range of inputs will yield more reliable predictions.

Launch

Models are only useful if we know how to use and interpret them!

  • Find the second section of Optimizing and Interpreting Linear Models: Interpreting the al-ak model.

  • Read the model interpretation with your partner and identify where the information on each of the fill in the blanks comes from.

  • Then answer the question.

  • How could we use the model to predict the median income for a state with a 30% college attendance rate?

  • Compute al-ak(30) by substituting 30 into the equation for x.

  • 5614 × 30 + 83616 = ~252306

Investigate

  • Turn to the third section of Optimizing and Interpreting Linear Models.

  • Using the interpretation of the al-ak model as a guide, write up your interpretation of the optimal model you just found for this dataset. Then answer the questions that follow.

For more practice, have students choose two other columns in the dataset to explore the relationship between and build linear models for using Building Models for Another Relationship in the Data.

Synthesize

  • When does it make sense to make an lr-plot?

  • When we’ve identified that the form of the data is linear

  • Our model is built from data about all of the existing states. College attendance rates range from 18.3% (West Virginia) to 52.4% (Washington, DC).
    Suppose two new states were to join the union, one with a 30% college attendance rate and the other with a 90% attendance rate. Is our model more reliable for one of these states than another? Why or why not?

  • This model is much more reliable for the 30% state than the 90% one!

  • A model is only as good as the data it was based on and the data in this dataset ranges from 18.3% to 52%.

  • If we could remove any row from this dataset to make our line fit better, which would you remove?

  • Washington, D.C. - it’s an outlier in virtually every measure!

  • Is it fair to remove that row? Why or why not?

  • Reason why: Washington, D.C. is a major metropolitan area! You can just erase those people to make the line fit better!

  • Reason why not: Washington, D.C. is not representative of the rest of the country at all. The unusual concentration of highly-educated people working for lower income is a special case because of all the government employees. Therefore, it’s ok to remove.

  • How could we use scatter plots and linear models to find answers to other questions, for example:

    • Do taller NBA players tend to make more three-pointers?

    • Do wealthier people live longer?

  • Find a dataset that contains the explanatory variable and response variable, import it into Pyret, and build an lr-plot!

Optional Activity: Guess the Model!

  1. Divide students into small groups (2-4), and have each team come up with a linear, real-world scenario, then have them write down a linear function that fits this scenario on a sticky note. Make sure no one else can see the function!

  2. On the board or some flip-chart paper, have each team draw a scatter plot for which their linear function is best fit. They should only draw the point cloud - not the function itself! Finally, students title their scatter plot to describe their real-world scenario (e.g. - "total cost vs. number of tickets purchased").

  3. Have teams rotate so that each team is in front of another team’s scatter plot. Have them figure out the original function, write their best guess on a sticky note, and stick it next to the plot.

  4. Have teams return to their original scatter plot, and look at the model their colleagues guessed. How close were they? What strategies did the class use to figure out the model?

    • The slope and y-intercepts can be constrained to make the activity easier or harder. For example, limiting these model settings to whole numbers, positive numbers, etc.

    • To extend the activity, have the teams continue rotating so that each group adds their sticky note for the best-guess model. Then do a gallery walk so that students can reflect: were the models all pretty close? All over the place? Were the guesses for one model setting more tightly than the guesses for another?

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: