Students investigating a dataset comparing wealth and median-life expectancy for countries of the world, and find the best linear, quadratic and exponential models they can to fit the data.
Lesson Goals |
Students will be able to…
|
Student-facing Lesson Goals |
|
Materials |
|
Preparation |
|
🔗Is Poverty Bad for Your Health?
Overview
Students explore the Countries of the World Starter File, and find a relationship between wealth and median life expectancy.
Launch

-
Countries measure their income in "Gross Domestic Product", which is often abbreviated "GDP". Many economists divide the total income for the country by the number of people living there, to estimate the average income of each person. This is called Per-Capita GDP.
-
Countries estimate how long-lived their citizens are by recording how long everyone lives, then taking the median of all those ages. This is called Median Life Expectancy.
We want to know if there a positive relationship between Per-Capita GDP and Median Life Expectancy. In other words: Do people in rich countries live longer?
-
In small groups, discuss and complete Do People in Rich Countries Live Longer?.
-
Be prepared to share your graphs, and why they look the way they do!
What graphs did you draw? Why do you think your graph accurately reflects the relationship between income and life-expectancy?
Investigate
Let’s take a look at some real data on income and life expectancy across the world.
-
Open the Countries of the World Starter File
-
From the File menu, select "Save a Copy", and click "Run".
-
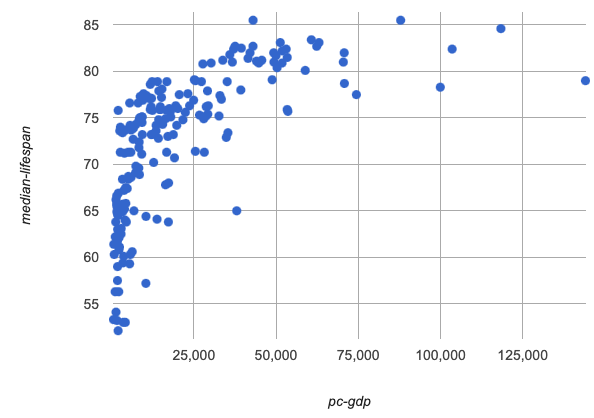
Make a scatter plot showing the relationship between
pc-gdpandmedian-lifespan, using the name of thecountryas the label. -
Working in pairs or small groups, complete Exploring the Countries Dataset.
-
What do you Notice?
-
What do you Wonder?
Discuss students' findings. Pay special attention to the terms students use to describe the pattern in the scatter plot. Is it linear, or something else? Are the points tightly clustered together, or more spread out? If there’s some disagreement among the students, that’s a good thing!
Synthesize
-
What is per capita GDP?
-
A widely used indicator of a country’s standard of living.
-
Per Capita GDP is calculated by dividing the GDP of a country by the population.
-
GDP stands for Gross Domestic Produce, which is a measure of the total economic performance of a country — a monetary measure of the total market value of all the final goods and services produced.
-
Would you expect increasing per capita GDP by $20,000 to increase life expectancy by the same amount for all of the countries in the world? Why or why not?
-
No. The first $20,000 or so of income shows a huge improvement in life expectancy: this might be enough to afford a place to live, see a doctor every once in a while, etc. But for wealthy countries with long life expectancies, more money is unlikely to raise their life expectancies by very much.
-
If a wealthy country is suffering heavy casualties in a war, where would we expect to see that country’s datapoint?
-
We would expect the dot to fall below the trend, because war is associated with deaths of young people.
-
What other conditions might cause a point to shift up or down?
-
Answers will vary! Some may include:
-
Life expectancy might drop as a result of extended drought, famine, pandemic, climate-related disasters, etc.
-
There aren’t very many scenarios that would rapidly increase the life expectancy of a country, other than reversal of the kind of crises described above.
-
Life expectancy might fall above the trend lines for countries with guaranteed income and universal healthcare.
-
🔗Linear? Quadratic? Exponential?
Overview
Students try to fit models they’ve seen before to the data.
Launch
How well do you think a linear model would fit this data? A quadratic one? Exponential?
Investigate
Make sure you have created a link or code for your class to Fitting Wealth-v-Health and Exploring Logarithmic Models (Desmos) and paced the class so they have access to the first 2 slides.
-
Open the Desmos link I’ve shared with you. (The file should be called Fitting Wealth-v-Health and Exploring Logarithmic Models.)
-
Working in pairs or small groups, complete Fitting Models for the Countries Dataset.
This activity involves lots of trial and error, as students try to come up with a good linear, quadratic, or exponential model.
The goal is to discover that a new kind of model is necessary, not to find a perfect fit with linear, quadratic, or exponential models!
-
What’s the best model you came up with?
-
What kinds of lines or curves did you draw?
-
How would you describe the shape of the scatter plot for
median-lifespanversuspc-gdp? -
It starts out rising fast on the left, put growth slows as
pc-gdpincreases to the right. -
How well did our linear, quadratic, and exponential models fit this data?
-
None of the kinds of functions we’ve seen so far exhibit the behavior we see here!
-
In some ways, this behavior is the exact opposite of exponentials: instead of starting slow and taking off like a rocket, this curve explodes up the y-axis right away, before leveling off.
Synthesize
What ideas do you have about the math that might make a sequence grow quickly at the beginning and then grow more slowly for larger x-values?
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927).  Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
