instagram

(Using another tool? Please select it now: CODAP.)

Students are introduced to mean, median and mode(s) and consider which of these measures of center best describes various quantitative data.

Lesson Goals

Students will be able to…​

  • Compute measures of center including mean, median and mode(s) of a dataset in Pyret.

  • Determine which measure of center – mean, median, or mode – best summarizes a dataset.

Student-facing Lesson Goals

  • Let’s use mean, median, and mode(s) to describe our data.

Materials

Supplemental Materials

Assessments

Preparation

  • Decide whether or not the first section of this lesson (an introduction to measures of center) is appropriate for your class.

    • Want to get a sense of what your students already know before you decide?

    • Looking for a do now to get the juices flowing before skipping ahead?

    • If you are teaching this section, each group of three students will need a ruler, a marker, tape, and 5 pennies for the kinesthetic activity.

    • If you are confident that your students have a solid understanding of mean, median, and mode(s), you can jump to the second section of the lesson, where students will use Pyret to compute measures of center, and then consider which measure of center is the most appropriate.

  • Decide whether or not you want to launch the second section of this lesson using the Live Pyret Survey and your class' own data. If so, follow the instructions on How to Use a Live Pyret Survey to:

  • If you are using our Google Slides, adjust the slides based on which portions of the lesson you will be doing with your students.

🔗Optional: Mean, Median, and Mode(s)

Overview

Students learn how to compute three different measures of center.

Launch

By the end of this section, students should be able to answer the questions on Mean, Median, Mode(s) Practice, which are the same as . Engage your students with this section at whatever speed and level of depth you deem appropriate for them or skip to the next if you’re confident they already know how to cumpute measures of center.

When working with dot plots, we often wondered, "What is a typical value in this sample?"

... and we often discovered that there were a variety of correct responses!

When thinking about typicality, there are a few approaches:

  • identify the value that is most common

  • identify the midpoint of the sample

  • identify a "balance point" among the data points

It turns out that these different ways of thinking about typicality are all different ways of "measuring the center".

Another way of asking "What value is typical?" would be "Is there a value that all the others tend to cluster around?"

Statisticians have a more formal, mathematically-defined term for this: central tendency. Central tendency is a "summary" measure, that attempts to describe a whole set of data with a single value that represents the middle or "center" of its distribution. In other words, a value that all the others tend to cluster around.

There are several different measures of central tendency. Data Scientists know what each measure is, and when to use it. And in the next few lessons, you’ll learn that too.

If you know that your students do not know how to compute mean, median, and mode(s), you can skip the first question, below.

  • Compute the mean, median, and mode for these datasets:

    • Dataset A:   17, 23, 24, 23, 22

    • Dataset B:   5, 5, 9, 9, 3, 29

    • Dataset C:   8, 34, 15, 4, 76

  • Solutions:

    • Dataset A…​ mean: 22; median: 23; mode: 23.

    • Dataset B…​ mean: 10; median: 7; modes: 5, 9.

    • Dataset C…​ mean: 27.4; median: 15; mode: none

  • Tell me everything you know about measures of center.

  • The goal of this question is to gauge students' general level of comfort with mean, median, and mode. Take notes on the board, which you can add to as students make additional discoveries about measures of center during the instruction.

Investigate

Mean

We can think of the mean as the balancing point of a dataset, or the value where the "weight" of all data points on one side is equal to the "weight" of all data points on the other side. Let’s explore this idea.

Divide the class into groups of three. Supply each group with a marker, a ruler, tape, and 5 pennies.

  • We are going to build a seesaw (also known as a teeter-totter) with a marker and a ruler.

  • Tape the marker flat onto your desk using two pieces of tape.

  • Set the ruler on top of the marker; try to balance it so that it hovers parallel to the surface of the desk.

  • To balance the ruler over the marker, where must the marker be positioned? Why?

  • The balance point is at 6 inches. There is an equal amount of weight on each side of the marker when it is placed at 6 inches.

  • Now, tape one penny at 1 inch and another penny at 11 inches. Did you need to change the location of the marker to keep the ruler balanced?

  • To balance the ruler, both pennies must be the same distance from the marker (or fulcrum). Both 11 and 1 are 5 units away from 6.

  • Keep the two pennies at 1 and 11, but tape a third penny at 9 inches. Adjust your ruler so that it hovers parallel to the desk. Did you need to change the location of the marker to keep the ruler balanced? Explain.

  • The ruler is balanced when the marker is at 10.5 inches. To balance the ruler, the total distance of the pennies below the balance point must add up to the distance of the penny above the balance point.

  • Tape the last penny onto a position of your choice. Find the balance point. Be prepared to share your results with the class.

  • We recommend drawing some sketches on the board of students' balanced rulers, adding and labeling arrows to represent the distance from each penny to the balance point.

  • The key idea is that the total distance from the mean to the lower data points must equal the total distance from the mean to upper data points.

Strategy: Building a Conceptual Understanding of Mean

Very commonly, students develop a computational understanding of mean, but not a conceptual one (Bakker et al, 2005Bakker, A., Biehler, R., & Konold, C. (2005). Should young students learn about box plots? In G. Burrill & M. Camden (Eds.), Curricular Development in Statistics Education: International Association for Statistical Education (IASE) Roundtable, Lund, Sweden, 28 June-3 July 2004., Pollatsek et al, 1981Pollatsek, A., Lima, S. & Well, A.D. Concept or computation: Students' understanding of the mean. _Educational Studies in Mathematics, 12, 191–204 (1981).). Without a strong conceptual understanding of mean, students will struggle to determine which measure of center is most appropriate in a given situation. We use activities recommended in the research (such as the kinesthetic one described above) to combat this misconception.

Interpreting the mean as the "fair share" can also help students think conceptually about mean. In other words: What amount will each member of a group get if everything is distributed equally? Sometimes, a thought experiment is most appropriate for conveying the "fair share" interpretation, e.g. if there are five dogs of differing weights, how would we redistribute the weight so that each of the five dogs is an equal weight? If you have students who struggle to think about mean as a balancing point, you might consider sharing this alternative interpretation.

To compute the mean of any dataset, we add up all of the values, and then divide by the number of values in the dataset. This algorithm reveals to us our balance point—​and we don’t even need the pennies, the ruler, or the trial and error!

  • Turn to Mean, Median, Mode(s) Practice and complete the first section of the page.

  • When you are finished, compare your answers with a partner’s answers and correct any mistakes.

Median

There is another measure of center we can use called the median. Instead of averaging the data points, it identifies the “middle” value, dividing the data into two groups. Half of the values are less than the median, and the other half are greater than median. In the image below, 40 Wall Street represents the median height of the dataset; three buildings are shorter, and three buildings are taller.

An infographic of the 6 tallest buildings (1908-1974) arranged by height, with the median value circled

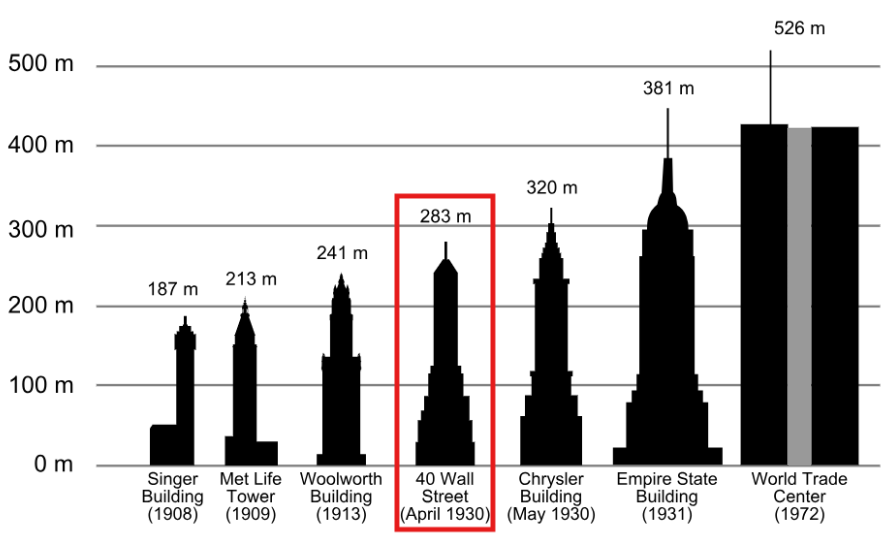
The algorithm for finding the median of a quantitative column is:

  1. Sort the numbers.

  2. Cross out the highest and lowest number.

  3. Repeat until there is only one number left.

  4. When there are an even amount number of numbers in the list, as in the example below , there will be two numbers left at the end. Take the mean of those two numbers.

Address the common misconception that the median is just a cut point in the data. Yes, the median is the middle value, but it is also a measure of center, meaning that it offers a characterization of the entire group of datapoints. Measures of center always summarize the values of a dataset with a single number.

Consider this list of ages: 25, 26, 28, 28, 28, 29, 29, 30, 30, 31, 32

Here 29 is the median. It’s the middle number of the list and it separates the "bottom half” (5 values below it) from the "top half” (5 values above it).

Now consider this list of ages: 3, 7, 9, 21

There is no middle number. So the median of this list will be the mean of the two middle numbers, 7 and 9, which is 8.

7 + 9 = 16 and 16 ÷ 2 = 8

Mode(s)

The third measure of center is called the mode(s) of a dataset. The mode(s) of a dataset are the values that appear most often.

Median and mean always produce one number and many datasets are what we call “unimodal”, having just one mode. But sometimes there are exceptions!

  • If all values are equally common, then there is no mode at all!

  • If two or more values are equally common, there can be more than one mode.

Consider the following three datasets:

1, 2, 3, 4
1, 2, 2, 3, 4
1, 1, 2, 3, 4, 4

  • The first dataset has no mode at all!

  • The mode of the second dataset is 2, since 2 appears more than any other number.

  • The modes (plural!) of the last dataset are 1 and 4, because 1 and 4 both appear more often than any other element, and because they appear equally often.

Can you find the mode(s) of this dataset?

red, green, red, yellow, blue, red, purple, purple

The mode here is red, which appears three times on the list. Highlight for students that yes, we can find the mode of a categorical dataset!

Synthesize

  • If you heard that the mean age of students in a kindergarten class was 21, would you be surprised? Why or why not?

  • Sample response: yes, that would be surprising. Usually students in kindergarten are 4 or 5 years old!

  • Is the median always one of the values in the dataset? If not, when is it not?

  • No, the median is not always one of the values in the dataset. Sometimes, when there are an even number of datapoints, we need to average the two middle values to find the median.

  • How come we can find the mode of a categorical dataset, but not the median or the mean?

  • Finding the mode does not require us to perform any arithmetic computations. Computing the median or the mean does require us to perform some arithmetic, therefore we can only use quantitative data.

🔗Choosing the Right Measure of Center

Overview

Students use Pyret to compute measure of center, and then consider which measure of center is most appropriate in a given situation.

Launch

Summarizing a big dataset means that some information gets lost, so it’s important to pick an appropriate summary.

Here are just a few examples of summary data being used for important things:

  • Students are sometimes summarized by two numbers — their GPA and SAT scores — which can impact where they go to college or how much financial aid they get.

  • Schools are sometimes summarized by a few numbers — student pass rates and attendance, for example — which can determine whether or not a school gets shut down.

  • Adults are often summarized by a single number — like their credit score — which determines their ability to get a job or a home loan.

  • When buying uniforms for a sports team, a coach might look for the most common size that the players wear.

Picking the wrong summary value (mean, median, or mode) can have serious implications!

Let’s learn how to use Pyret to quickly, easily compute the three different measures of center so the we can spend our energy thoughtfully deciding which measure of center is the most appropriate in a given situation, rather than number crunching.

If you decided to launch today’s class using our Live Pyret Survey, now is the time!

When you click "Run", the Minutes it took to get to school this morning (Starter File) displays the mean, median and mode(s).

Assuming you’ve already…​

  1. Followed the Instructions to Set up and Link the Files

  2. Shared the link you made to your class' copy of the Minutes it took to get to school this morning (Google Form)

The data visualizations will be generated using data from your students!
And they will continue to update in real time as more of your students complete the Google Form.

Project your screen and/or publish the starter file and share a link with your students.

Facilitate a discussion about this new-to-them Pyret Data Visualization!

  • If you haven’t already done so, open the Google Form Survey link I shared and submit your response.

  • Then look at the Survey Results being displayed on the Board.

  • What do you Notice?

  • What do you Wonder?

Investigate

Pyret has functions that will compute mean, median, and mode.

# mean :: Table, String -> Number

# median :: Table, String -> Number

# modes :: Table, String -> List

Note: List is a new data type!

  • Why do you think modes returns a List?

  • If modes only returned a Number, there would be no way to indicate if there are multiple modes.

  • Open the Animals Starter File in Pyret.

  • Complete Choosing the Best Measure of Center, using Pyret to compute and record all three measures of center for the pounds column. Write your responses on the table in question 1.

  • Respond to the remaining questions using the information you have recorded on the table.

Question 3 requires students to apply their knowledge of mean and median, which can be quite difficult. Commonly, students' understanding of center does not extend beyond algorithms. Invite students to think back to what they know about histograms and histogram shape. Challenge them to think deeply about how a histogram’s shape relates to its measures of center. We will continue to consider this topic in the next lesson section.

Let’s summarize some of the key ideas we encountered while thinking about the best measure of center to summarize the pounds column of the animals dataset.

  • When is mean probably the best measure of center to use?

  • The mean is a useful summary number when all of the points in a dataset are fairly balanced on either side of the middle.

  • Although mean is generally the best measure of center, statisticians sometimes fall back to the median. When is median the best measure of center to use?

  • For skewed datasets, the median is a better summary value because it is less sensitive to skew. Mean is misleading for datasets with imbalance and extreme outliers.

  • In what situations is mode the best measure of center?

  • The mode is a useful measure of center when we have a dataset with a small number of values. Mode is also our only measure of center that can be used with categorical data.

Consider how many policies or laws are informed by statistics! Knowing about measures of center helps us see through and critique misleading statements.

Synthesize

  • Do you trust this statement?: In 2003, the average American family earned $43,000 a year — well above the poverty line! Therefore, very few Americans were living in poverty. Why or why not?

  • Sample response: The mean is sensitive to outliers, and billionaires like Elon Musk, Jeff Bezos, etc. pull the mean heavily to the right. This makes it appear that the "average" American family earns far more than they actually do. That’s why the conclusion "very few Americans were living in poverty" cannot be drawn based on the mean.

  • Given the extreme income inequality in the United States, what measure of center would best represent a typical family income?

  • The median

🔗Data Exploration Project (Measures of Center)

Overview

Students apply what they have learned about measures of center to their chosen dataset, completing the first four rows of the "Measures of Center and Spread" table in their Data Exploration Project Slide Template. They will also interpret those measures of center, and record any interesting questions that emerge.

Visit Project: Dataset Exploration to learn more about the sequence and scope. Teachers with time and interest can build on the exploration by inviting students to take a deep dive into the questions they develop with our Project: Research Capstone.

Launch

Let’s review what we have learned about computing and interpreting three measures of center - mean, median, and mode(s).

  • Describe how to compute mean, median, and mode(s).

  • When does mean provide the best summary?

  • It includes information from every single point, so it is useful when the data doesn’t show much skewness or have outliers.

  • When does median provide the best summary?

  • Statisticians fall back to the median when working with highly skewed datasets.

  • When are mode(s) a useful way to summarize a dataset?

  • Mode(s) are most useful when a dataset has very few values.

Investigate

Let’s connect what we know about measures of center to your chosen dataset.

Students have the opportunity to choose a dataset that interests them from our List of Datasets in the Choosing Your Dataset lesson. If you’d prefer to focus your class on a single dataset, we recommend the Global Food Supply & Production Starter File.

Complete two Data Cycles that use measures of center to help you analyze and understand your chosen dataset.

Invite students to discuss their results and consider how to interpret them.

It’s time to add to your Data Exploration Project Slide Template.

  • Locate the "Measures of Center and Spread" section of your Exploration Project and, in the slide following the example, replace Column A with the title of the column you just investigated.

  • Then type in the mean, median and mode(s) that you just identified. Leave the other rows blank. We will come back to them another day.

  • On the next slide, repeat with Column B using the second column you’re interested in.

  • Add your interpretations to the two "Measures of Center and Spread" slides.

  • Record any questions that emerged in the "My Questions" section at the end of the slide deck.

Synthesize

Have students share their findings.

  • Did you discover anything surprising or interesting about your dataset?

  • Which measures of center do you think were the most useful for the quantitative columns you chose?

  • What questions did the measures of center inspire you to ask about your dataset?

  • When you compared your findings with other students, did you make any interesting discoveries? (For instance: Did everyone find mode(s)? Did anyone have a measure of center that was dramatically influenced by an outlier?)

🔗Additional Exercises

- Matching Modes (Desmos)

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: