Students explore the concept of linear relationships, as represented in tables and graphs.
Lesson Goals |
Students will be able to…
|
Student-facing Lesson Goals |
|
Materials |
|
Preparation |
|
Key Points for the Facilitator |
|
Supplemental Resources |
- linear
-
a rule that computes one quantity from another, which can be graphed as a straight line or written as a sequence of numbers that change at a constant rate
🔗Simple Sequences and Straight Lines 35 minutes
Overview
Students explore the concept of linearity, as represented in tables and graphs.
Launch
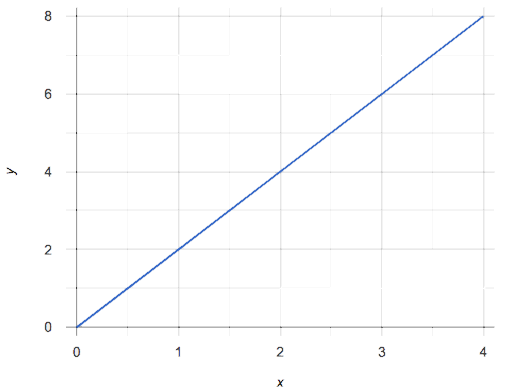
Take a look at the following rows in a table and points on a graph:
|
-
What do you Notice?
-
What do you Wonder?
Each row in the Table represents an (x, y) point on the graph. The "x" column is a list of positions along the x-axis, and the "y" column is filled with values that are computed from those position according to some rule.
Can you predict the next two rows in the table? The next points on the graph? How did you arrive at your prediction?
The y-column in the table and the y-coordinates on the graph follow a rule, which dictates how y relates to x. When x goes up or down by 1, y goes up or down by 2. We expect that rule to continue for all values of x, continuing the line and extending the table in both directions, forever.
Linear Relationships: Sequences that change at a constant rate, or points forming a straight line on a graph.
Rules that behave this way are called linear relationships. In a linear relationship, the y-values in a table change by the same amount between x-values. In a linear relationship, the y-coordinates change by the same amount between x-coordinates - drawing a straight line on the graph.
Linear relationships are everywhere:
-
"A car is traveling at 50 miles per hour"
-
"Milk costs $2.50 per gallon"
-
"There are 18 wheels on every tractor-trailer"
-
"A tree grows 2 inches each year"
-
"There are 30 students per teacher"
-
What other linear relationships can you think of?
-
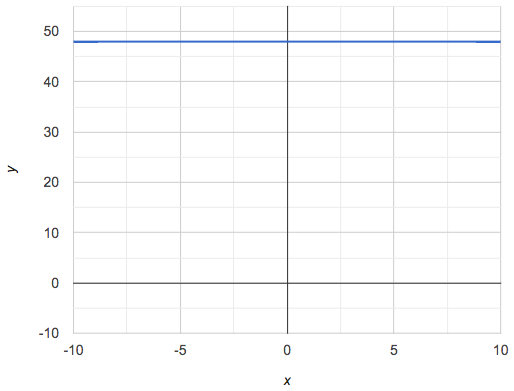
Imagine of a horizontal, straight-line relationship where y = 3 ("for all values of x, y is three"). Is this linear? By what amount is y changing between x-values?
-
Now imagine a vertical, straight-line relationship where x = 3 ("for all values of y, x is three"). Is this linear?
Linear Functions: linear rules that only work from x to y.
A linear relationship can exist from x-to-y, or from y-to-x. The last two relationships listed above are both linear!
But a linear function is strictly x-to-y. We can also describe this as "input-to-output", or "Domain to Range." Not all linear relationships are linear functions! Linear functions can only have one possible y-value for a single x-value, so our horizontal line fx = 3 can be written as a function but our vertical line fy = 3 cannot.
Investigate
Look at the two "sideways" data tables below.
|
|
-
What do you Notice?
-
What do you Wonder?
-
Can you figure out what the next (x,y) pair should be for each of them?
-
Can you guess what the y-value for each table would be when x is 0?
We can think of the "x" column as counting the order in which the y-values appear (1st value, 2nd value, etc). The "y" column, on the other hand is computed from the x-values according to some function.
When there is a linear relationship, the y-values change at a constant rate. If we were to graph those values, all of the points would fall on a straight line.
-
Complete Matching Tables to Graphs (Desmos).
-
Optional: Complete Matching Tables to Graphs.
Pedagogy Note To encourage students to look at the points in the table and graph, it is useful to change the scale of the graphs so that all lines look the same. This prevents students from leaning on visual cues like "steepness" to bypass the learning objective. It can also be useful to list the points in the table out of order, both to focus students' attention on the points and to drive home that rows do not have to be ordered! |
Axes on a graph need an order. Rows in a table don’t!
The rows in a table are discrete. They preserve their meaning if the rows are shuffled into a different order. Ordering the rows in a table can make it easier for us to find the function.
In a graph, the points on the x-axis cannot be shuffled, because the x-axis must always be ordered. We can stretch the scale of the axes to making the lines look different, but the points will always be in the same order.
Can you match tables and graphs, even if the rows are shuffled and the axes are changed? Complete Matching Tables to Graphs 2.
Synthesize
Linear relationships show up all the time in real life, so it’s helpful to know how to think about them. We’ve seen that linear relationships can be represented as tables and graphs. Tables only show us some points on a line, whereas a line itself is made up of an infinite number of points. While a table represents a sample of some larger trend, the graph is a way of seeing the trend itself.
🔗Linear, Non-Linear, or Bust! 20 minutes
Overview
Students deepen their understanding of linearity, by seeing counterexamples (non-linear relationships), as well as tables and graphs for which there is no relationship.
Launch
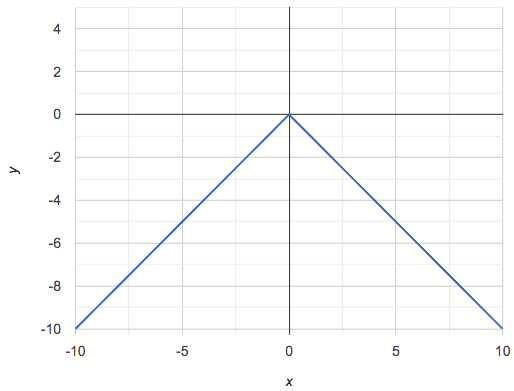
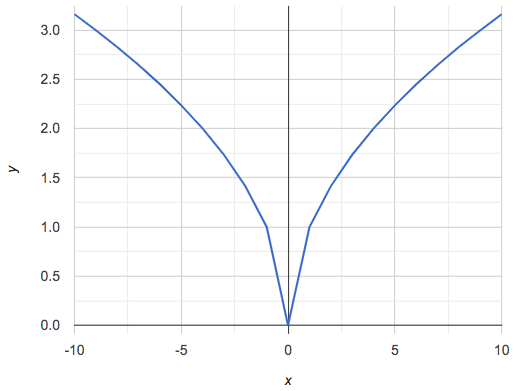
If all linear relationships can be shown as points on a graph, does that mean all graphs are linear? Look at the six graphs shown below:
-
What do you Notice?
-
What do you Wonder?
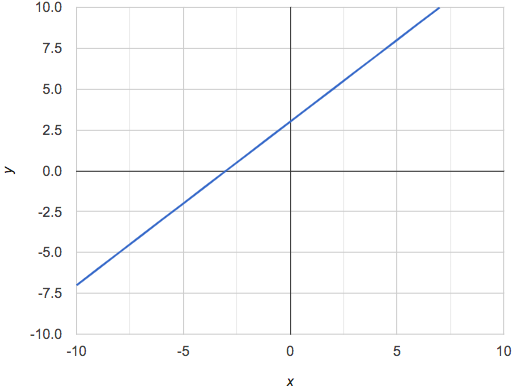
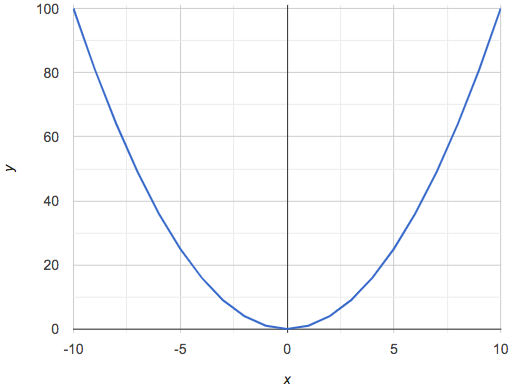
Three of the graphs above show linear functions, and three show other, non-linear functions. As we can see, the linear graphs can be perfectly horizontal, slope upwards and to the right, or slope downwards to the right. NOTE: there are still clearly patterns in the non-linear relationships — they just aren’t linear!
Linear relationships in a graph always appear as straight lines
If all linear relationships can be shown as a tables, does that mean all tables are linear? Look at the six tables shown below:
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
-
What do you Notice?
-
What do you Wonder?
-
Can you figure out what the next x,y pair should be for each of them?
-
Can you guess what the y-value for each table would be when x is 0?
Three of the tables above show a linear function, and three show other, non-linear functions. As we can see, the linear tables can have y-values that change by zero (no change), by a positive number (constant increase), or a negative number (constant decrease). NOTE: there are still clearly patterns in the non-linear relationships — they just aren’t linear!
Linear relationships in a table show up as sequences that change at a constant rate. The y-value when x is zero is also the value where the line will cross the y-axis.
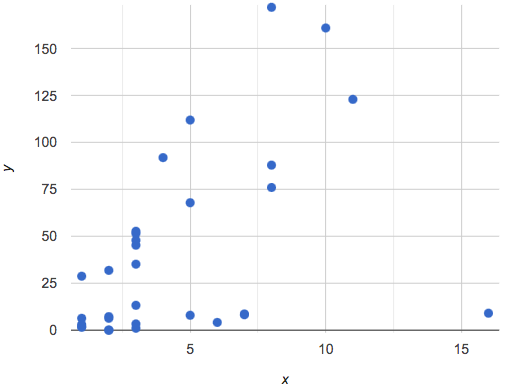
Sometimes there is no function that will give us a particular table or graph! Take a look at the table and points below. Can you predict the next two rows? Where will the next point be?
|
Vertical Line Test: If there are two different y values for the same x, it can’t be a function!
Think back to our vertical line fy = 3: x is three all the time, for an infinite number of y-values. If multiple y-values come from the same x-value, we know it’s not a function. In math books, this is called the vertical line test.
🔗Investigate
Can you tell when a relationship is a linear function? A non-linear one? Not a function at all?
-
Complete Linear, Non-linear, or Bust?
-
Optional: Complete Graphs: Linear, Non-linear, or Bust?
Synthesize
Data has a "shape", and this shape can emerge when we look for patterns in that data. A linear function is one kind of pattern, and we can see it when viewing data as a table or a graph.
🔗Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598). 
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.