Standards (click one) |
Common Core Math Standards
CSTA Standards
Oklahoma Standards
|
Students apply their knowledge of the Pythagorean Theorem and Circles of Evaluation to develop a function for the distance formula.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-Facing Lesson Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Supplemental Resources |
|
|||||||||||||||
Preparation |
|
|||||||||||||||
Key Points for the Facilitator |
|
|||||||||||||||
Language Table |
|
Click here to see the prior unit-based version
- circle of evaluation
-
a 'sentence diagram' of the structure of a mathematical expression
- coordinate
-
a number or set of numbers describing an object’s location
- interactions area
-
the right-most text box in the Editor, where expressions are entered to evaluate
🔗Distance in 1 Dimension 15 minutes
Overview
Students discover the need for distance calculation (first in one dimension, then in two) in video games.
Launch
Students should have their workbook, pencil, and be logged into WeScheme on their computer.
Open your saved Game File, which should have the Target and Danger moving on their own. Your Player should respond to keypresses, and the Target and Danger should re-appear after they leave the screen. It’s almost fully-playable!
-
What seems to be missing from this game?
The characters aren’t doing anything when they collide.
-
What does it mean for characters to 'hit' one another? To collide?
They have to be close enough to touch.
-
How will the computer know when the characters have collided?
When the coordinates of the characters are really close to each other.
Scroll down to the distances-color definition (look for ; 4. Collisions in the file). Right now this value is defined to be the empty string "". Change this to a color that will show up on your background, and click "Run".
This setting will draw lines from your Player to each of the other characters, and then use those lines as the hypotenuse of right triangles!
The legs of these triangles show the distance in 1 dimension each (on the x- and y-axis). How is this calculated?
Role-Play: Ask a volunteer to help role-play two characters colliding!
-
Identify a "number line" on the floor (this can be done just by pointing, or with a visual aid).
-
Make sure that you and your volunteer stand with feet as close together as possible, representing the infinitely small point that identifies your center.
-
Raise your arms to form a "T shape", representing the outer edges of the characters.
-
Emphasize that this represents one dimension (perhaps the x- or y-axis).
-
With the volunteer, stand about 10 steps away from one another and side-step towards each other one step at a time, while asking the class, "True or False? We are colliding!" Be sure to only accept "true" and "false" as responses - not "yes" and "no"!
-
Ask the class how far apart you and your volunteer are, and then ask them how they would calculate this if you were standing on a number line and they could see the actual coordinates under your feet.
-
After a few iterations, try switching places and repeating. Point out that students always subtract the smaller number from the larger one, regardless of the character order!
-
Do this until students can clearly see it’s when the two characters are 'touching' or 'overlapping' in some way - NOT when they are 'at the same point.'
Investigate
Let’s explore how the program computes the length of these lines…
Have students find the line-length function in their game files, click Run, and practice using it in the Interactions area with different values for a and b.
Extension
You can extend this |
-
What does this function do?
-
Why does it use conditionals?
Synthesize
Make absolutely certain that students understand that this function always returns the positive distance between two points on a number line.
What if we have points that are not on the same line? What if instead they differ by both the x- and y-coordinate?
🔗Distance in 2 Dimensions 30 minutes
Overview
Students extend their understanding of distance from one dimension to two, using a geometric proof of the Pythagorean Theorem to compute the distance between two points.
Launch
🖼Show image
Bring your volunteer (or choose a different one!) back up to the front of the class, and have them squat down on the floor to represent a difference in the y-coordinate between the player and a character. Repeat the role-play activity.
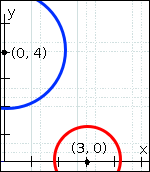
Suppose the Player is at (0, 4), and another game character is at (3, 0). Now there is a difference in both dimensions. How could we calculate distance now?
Computing the distance in 1-dimension is great, as long as the Player and Danger have the same x- or y-coordinate. In that case, the difference between the coordinates is exactly the distance between the two characters. But how do we compute the distance between two points when both the x- and y-coordinates are different?
Have students watch video of this problem [Credit: Tova Brown], and try explaining the proof to one another. In our case, the lengths A and B are computed by the line-length function we already have!
Have students write code to find the distance between these game characters Writing Code to Calculate Missing Lengths (Page 81).
Why line-length? Students learn early on that distance in 1-dimension is computed via \lvert x_2 - x_1 \rvert, and that distance is always a positive value. The Pythagorean Theorem teaches students that the length of the hypotenuse is computed based on the distance in the x- and y-dimension. However, most math textbooks show the distance formula without connecting back to that formula: √( ( (x_2 - x_1) )^2 + ( (y_2 - y_1) )^2 ) A student who asks whether it’s a problem when x_2 - x_1 is negative is displaying a deep understanding of what’s going on. Unfortunately, the response to this student relies on a computational artifact of squaring to force a number to be positive (rather than the purpose of squaring in the Pythagorean Theorem). Using the √( ( \lvert x_2 - x_1 \rvert )^2 + ( \lvert y_2 - y_1 \rvert )^2 ) |
Investigate
Turn to Distance on the Coordinate Plane (Page 82) and look at how line-length is used in the code. See if you can figure out how to write the code for the second problem.
Turn to The Distance Between (0, 2) and (4, 5) (Page 83) in your student workbook. Convert this expression to a Circle of Evaluation, and then to code.
Optional: Have students use this Multiple Representations: Distance between two points (Page 84) to model the distance formula for these coordinates with the Circles of Evaluation.
Practice computing the distance between two different points, by completing Distance From Game Coordinates (Page 85).
Optional: Have students complete another pair of these problems using Distance From Game Coordinates 2
Debrief these workbook pages - or have students pair-and-share - before moving on to writing the full distance function.
Using Distance (px, py) to (cx, cy) (Page 86), write a function that takes in two coordinate pairs (four numbers) of two characters (x_1, y_1) and (x_2, y_2) and returns the distance between those two points. HINT: the code you wrote in The Distance Between (0, 2) and (4, 5) (Page 83) can be used to give you your first example!
Students can test their distance function using Pythagorean triples, such as (3, 4, 5) or (5, 12, 13), to make sure the function is calculating the distance correctly. Finally, students fix the broken distance function in their game files. When they click "Run", the right triangles will appear with proper distances for the hypotenuse.
If we knew the lengths of the hypotenuse and one leg of the triangle, could we use the formula A^2 + B^2 = C^2 to compute the length of the other leg?
Take a look at the two examples on Comparing Code: Finding Missing Distances (Page 87). There’s a subtle difference between the two examples! What is it? Can you explain why they need to be written differently?
Common Misconceptions
It is extremely common for students to put variables in the wrong order. In other words, their program looks like
…(sqrt (+ (sqr (line-length x1 y1)) (sqr (line-length x2 y2))))…
instead of …(sqrt (+ (sqr (line-length x2 x1)) (sqr (line-length y2 y1))))…
In this situation, remind students to look back at what they circled and labeled in the examples step. This is why we label!
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598). 
Bootstrap:Algebra by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.