Standards (click one) |
Common Core Math Standards
Oklahoma Standards
|
Students identify solutions and non-solutions of inequalities using an interactive starter file. This lesson also reviews the Boolean datatype.
Lesson Goals |
Students will be able to:
|
|||||||||||||||
Student-Facing Lesson Goals |
|
|||||||||||||||
Materials |
||||||||||||||||
Preparation |
|
|||||||||||||||
Supplemental Resources |
||||||||||||||||
Key Points for the Facilitator |
|
|||||||||||||||
Language Table |
|
- Boolean
-
a type of data with two values: true and false
- data types
-
a way of classifying values, such as: Number, String, Image, Boolean, or any user-defined data structure
🔗Introducing Booleans 20 minutes
Launch
Students should be logged into WeScheme
Ask students to evaluate Circles of Evaluation for simple expressions they’ve seen before, and ask them to convert them into code.
-
+ 1 2 (+ 1 2) -
- 4 5 (- 4 5) -
* 8 0 (* 8 0)
Then show them unfamiliar Circles of Evaluation, and ask them to hypothesize what they think they mean, what they will evaluate to, and what the code would look like.
-
> 1 2 (> 1 2) -
< 4 5 (< 4 5) -
= 8 0 (= 8 0)
Have students convert these Circles to code and type them in. What did they evaluate to? What do they think the outputs mean?
Values like true and false obviously aren’t Numbers or Images. But they also aren’t Strings, or else they would have quotes around them. We’ve found a new data type, called a Boolean.
Investigate
Have students open the Boolean Starter File (Wescheme)
-
Explore the five functions in this starter file:
odd?,even?,less-than-one?,continent?,primary-color? -
All five functions produce Booleans. Through your exploration, see if you can come up with an explanation of what a Boolean is.
A Boolean is just another data type, like Numbers or Images. But unlike the others there are only two values: true and false.
-
Turn to Boolean Functions (Page 65) and use the starter file to complete the questions, identifying inputs that will make each function produce
true, and inputs that will make each functionfalse.
Synthesize
-
Students will see functions on this page that they’ve never encountered before! But instead of answering their questions, encourage them to make a guess about what they do, and then type it in to discover for themselves.
-
Explicitly point out that everything they know still works! They can use their reasoning about Circles of Evaluation and Contracts to figure things out.
Common Misconceptions
-
Many students - especially traditionally high-achieving ones - will be very concerned about writing examples that are "wrong." The misconception here is that an expression that produces
falseis somehow incorrect. You can preempt this in advance, by explaining that our Boolean-producing functions should sometimes return false.
🔗Introducing Inequalities 20 minutes
Overview
Students discover (or expand their understanding of) inequalities by identifying solutions and non-solutions and connecting expressions to graphic representations.
Launch
Have students open the Simple Inequalities Starter File. (Wescheme)
Equations typically have finite solution sets: there’s only one answer for an unknown, or perhaps several answers. Inequalities, on the other hand, can have infinite solutions. Inequality expressions divide all of the numbers in the universe into two categories: solutions and non-solutions. It is important that students are able to recognize that there are many possible solutions and non-solutions to an inequality and that they can identify whether or not a given number is or isn’t part of the solution set.
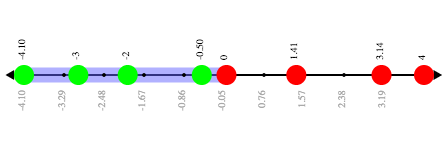
This starter file includes a special inequality function that takes in a function, which tests numbers in an inequality, a list of 8 numbers (to test in the function), and plots the numbers and a graph of the inequality on a number line.
The solution set is shaded in blue, with points shaded green (solution) and red (non-solution).
The resulting plot shows the number line, with all solution values shaded in blue. The 8 numbers provided in the list are shown as green (solution) or red (non-solution) circles. A successful input will include 4 solutions and 4 non-solutions, so the image returned will show 4 green dots and 4 red dots.
If their list of 8 values doesn’t include an equal number of solutions and non-solutions there will be an unequal distribution of red and green dots and they will get an error message encouraging them to adjust their list.
Encourage students to use negatives, positives, fractions and decimals as they generate their lists.
The starter file includes an example. Read the example code in the file carefully and click run to see the image it returns. Discuss the code with your partner.
-
What do you Notice?
-
What do you Wonder?
Hiding Example Code In order to stop seeing the examples written into the starter file code, students can comment out the example code by adding a # in front of each of the lines they want to hide. |
Investigate
Have students open to the Simple Inequalities (Page 66) and complete it with a partner, identifying solutions and non-solutions to each inequality and testing them in the Simple Inequalities Starter File. (Wescheme)
Synthesize
-
What patterns did you observe in how the inequalities worked?
🔗Additional Exercises:
These materials were developed partly through support of the National Science Foundation,
(awards 1042210, 1535276, 1648684, and 1738598). 
Bootstrap:Algebra by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.